Computer Science/Python

파이썬 | 시간 복잡도(Time Complexity), Big O, O(n), O(n^2), O(1), O(log n), O(a + b)

올리브한입 2024. 9. 21. 13:18
반응형

시간 복잡도(Time Complexity)란?

시간 복잡도는 알고리즘이 실행되는 데 걸리는 시간을 입력 크기 n에 따라 분석하는 방법입니다. 이는 알고리즘의 효율성을 평가하는 중요한 요소 중 하나로, 입력 데이터가 커질수록 실행 시간이 어떻게 변하는지를 측정합니다. 일반적으로 시간 복잡도는 Big O 표기법을 사용하여 나타냅니다.

Big O, Big Omega, Big Theta

시간 복잡도에는 크게 세 가지 종류의 표기법이 있습니다.

  1. Big O (O): 알고리즘의 최악의 경우를 나타냅니다. 이는 입력 크기가 커질 때, 알고리즘이 소요할 수 있는 최대 실행 시간을 뜻합니다. 우리는 보통 Big O에 집중하여, 최악의 경우 성능을 평가합니다.
  2. Big Omega (Ω): 알고리즘의 최선의 경우를 나타내며, 최소한 이 정도의 시간이 걸린다는 하한선을 의미합니다.
  3. Big Theta (Θ): 알고리즘의 평균적인 경우를 나타냅니다. 이는 최악의 경우와 최선의 경우가 동일한 상황에서 사용됩니다.

알고리즘 성능 분석에서는 보통 Big O에 집중합니다. 왜냐하면 알고리즘이 최악의 상황에서도 효율적으로 작동하는지 평가하는 것이 중요하기 때문입니다.

O(n) 예시

def print_items(n):
    for i in range(n):
        print(i)

print_items(10)
[Running] 
0
1
2
3
4
5
6
7
8
9

[Done] exited with code=0 in 0.762 seconds

 

이 함수의 시간 복잡도는 O(n)입니다. 왜냐하면 n개의 항목을 출력하기 위해 n번 반복하기 때문이죠. 입력 크기 n이 커질수록 반복문의 실행 횟수도 동일하게 증가합니다. 예를 들어, 입력 크기가 10일 때는 10번의 연산이, 100일 때는 100번의 연산이 일어납니다. 

def print_items(n):
    for i in range(n):
        print(i)

    for j in range(n):
        print(j)

print_items(10)

 

이 코드의 시간 복잡도도 O(n)입니다. 이 코드에서는 두 개의 for 반복문이 있습니다.

  1. 첫 번째 for i in range(n)는 i가 0부터 n-1까지 반복하며, n번의 연산을 수행합니다.
  2. 두 번째 for j in range(n)도 동일하게 n번의 연산을 수행합니다.

따라서, 이 코드에서 총 실행되는 연산의 횟수는 n + n, 즉 2n입니다.

 

그러나 Big O 표기법에서는 상수는 무시합니다

Big O 표기법은 입력 크기 n이 커질 때의 동작을 평가하는 방식입니다. 상수 배수는 성능에 큰 영향을 주지 않으므로, 2n에서 상수 2를 무시하고 최종적으로 시간 복잡도를 O(n)으로 표기합니다.

 

O(n^2) 예시

def print_items(n):
    for i in range(n):
        for j in range(n):
            print(i, j)

print_items(5)
[Running] 
0 0
0 1
0 2
0 3
0 4
1 0
1 1
1 2
1 3
1 4
2 0
2 1
2 2
2 3
2 4
3 0
3 1
3 2
3 3
3 4
4 0
4 1
4 2
4 3
4 4

[Done] exited with code=0 in 0.079 seconds
  1. 첫 번째 for i in range(n): i는 0부터 n-1까지 반복되며, 총 n번 실행됩니다.
  2. 두 번째 for j in range(n): 이 반복문은 매번 i가 실행될 때마다 n번 실행됩니다.

즉, i가 1번 실행될 때마다 j는 n번 실행되고, 전체적으로 n번의 반복문이 중첩되어 실행되므로, 최종적으로 n * n = n²번의 연산이 일어납니다. 따라서 시간 복잡도는 O(n²)입니다.

def print_items(n):
    for i in range(n):
        for j in range(n):
            print(i, j)

    for k in range(n):
        print(k)

이 경우는 중첩된 반복문과 독립된 반복문이 혼합되어 있는 경우로, 각 부분의 복잡도를 따로 계산한 후 전체 시간 복잡도를 구할 수 있습니다. 

for i in range(n):
    for j in range(n):
        print(i, j)

 

  • for i in range(n)는 n번 실행됩니다.
  • 각 i에 대해 for j in range(n)는 n번 실행되므로, 이 중첩 반복문은 총 n * n = n²번 실행됩니다.
  • 이 부분의 시간 복잡도는 O(n²)입니다.
for k in range(n):
    print(k)
  • 이 반복문은 독립적으로 n번 실행되므로, 시간 복잡도는 O(n)입니다.

Big O 표기법에서는 가장 큰 성능에 영향을 주는 요소만을 고려하므로, O(n²)가 O(n)보다 성능에 더 큰 영향을 미칩니다. 따라서 전체 시간 복잡도는 O(n²)로 표현됩니다.

 

O(1) 예시

def add_items(n):
    return n + n + n

 

이 코드의 시간 복잡도는 O(1), 즉 상수 시간 복잡도입니다. 코드의 동작을 분석해보면, 입력 크기 n에 관계없이 항상 동일한 연산을 수행하기 때문입니다. 

 

  • n + n + n은 세 개의 더하기 연산이 수행됩니다.
  • 이 연산은 n의 크기와 상관없이 항상 3번의 덧셈만 수행되므로, 입력 크기가 커져도 실행 시간에 변화가 없습니다.

 

O(log n) 예시

 

O(log n) 시간 복잡도는 알고리즘이 입력 크기가 커질수록 성능이 로그 형태로 증가하는 경우를 의미합니다. 대표적인 예로 이진 탐색(Binary Search)을 들 수 있습니다. 리스트에서 특정 값을 찾을 때, 리스트를 반으로 나눠가며 탐색하기 때문에 O(log n)의 시간 복잡도를 가집니다.

 

예를 들어, 정렬된 리스트에서 이진 탐색(Binary Search)을 사용하여 숫자 1을 찾는 과정을 설명해보겠습니다.

1 2 3 4 5 6 7 8

리스트에서 숫자 1을 찾으려면, 먼저 리스트를 반으로 나눕니다. 

1 2 3 4

1은 4보다 작으니까, 앞쪽 절반만 남기고 나머지는 무시합니다. 남은 절반에서 또 중간값을 찾습니다.

1 2

1은 2보다 작으니까, 앞쪽 절반만 남깁니다. 같은 방식으로 숫자 1을 찾아냅니다.

1

 

정리하면

  • 리스트 [1, 2, 3, 4, 5, 6, 7, 8]의 크기는 8 (n = 8).
  • 첫 번째 단계: 리스트를 반으로 나누어 4개의 요소가 남습니다.
  • 두 번째 단계: 다시 반으로 나누어 2개의 요소가 남습니다.
  • 세 번째 단계: 또 반으로 나누어 1개의 요소가 남습니다.

이처럼 리스트 크기가 8에서 1이 되기까지 총 3단계를 거쳤습니다. 이는 log₂(8) = 3과 일치합니다. 리스트 크기가 커질수록 탐색 단계가 늘어나지만, 선형적으로 늘어나지 않고 로그 형태로 증가하게 되는 것이 O(log n) 시간 복잡도의 의미입니다.

 

O(a + b) 예시

def print_items(a, b):
    for i in range(a):
        print(i)

    
    for k in range(b):
        print(k)

 

  1. 첫 번째 반복문 (for i in range(a)):
    • 이 반복문은 i가 0부터 a-1까지 반복됩니다.
    • 즉, 이 부분은 a번 실행됩니다.
  2. 두 번째 반복문 (for k in range(b)):
    • 이 반복문은 k가 0부터 b-1까지 반복됩니다.
    • 즉, 이 부분은 b번 실행됩니다.

첫 번째 반복문은 O(a), 두 번째 반복문은 O(b)의 시간 복잡도를 가집니다. 두 반복문이 독립적이기 때문에, 전체 시간 복잡도는 O(a + b)로 계산됩니다. 두 개의 다른 변수가 각각 따로 작동하기 때문에, 이를 합산하여 나타냅니다.

 

리스트의 주요 연산에 대한 Big O 시간 복잡도

1. 접근 (Access)

  • 연산: list[i]
  • 시간 복잡도: O(1)
  • 설명: 특정 인덱스에 직접 접근할 수 있기 때문에 항상 일정한 시간에 요소를 가져올 수 있습니다.

2. 삽입 (Insert)

  • 연산: list.insert(index, value)
  • 시간 복잡도: O(n)
  • 설명: 특정 인덱스에 요소를 삽입할 때, 그 뒤에 있는 모든 요소를 이동시켜야 하므로 리스트 크기 n에 비례하여 시간이 소요됩니다.

3. 추가 (Append)

  • 연산: list.append(value)
  • 시간 복잡도: O(1)
  • 설명: 리스트의 끝에 요소를 추가하는 작업은 항상 일정한 시간에 수행됩니다.

4. 제거 (Remove)

  • 연산: list.remove(value) 또는 list.pop(index)
  • 시간 복잡도:
    • O(n) (특정 값을 제거하는 경우, 리스트 전체를 검색해야 할 수도 있음)
    • O(1) (맨 마지막 요소를 pop할 경우)

5. 슬라이싱 (Slicing)

  • 연산: list[start:end]
  • 시간 복잡도: O(k) (여기서 k는 슬라이스된 요소의 수)
  • 설명: 부분 리스트를 생성할 때, 해당 요소들을 복사해야 하므로 슬라이스의 크기에 비례하여 시간이 소요됩니다.

6. 검색 (Search)

  • 연산: value in list
  • 시간 복잡도: O(n)
  • 설명: 리스트를 순차적으로 검색해야 하므로, 리스트의 크기에 비례하여 시간이 소요됩니다.

요약

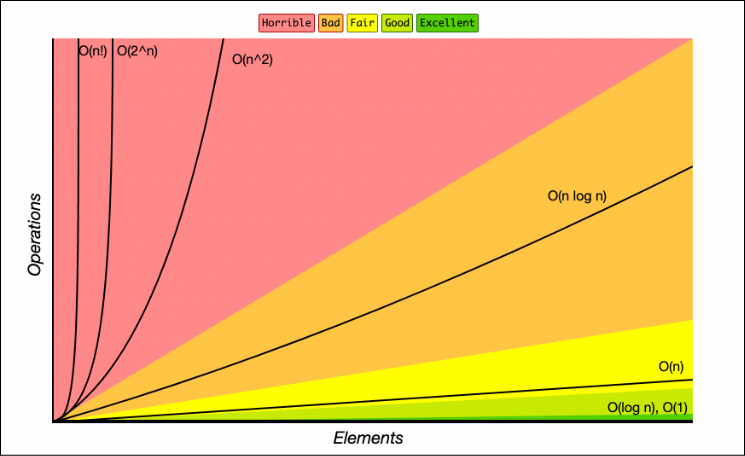
https://www.freecodecamp.org/news/big-o-cheat-sheet-time-complexity-chart/

O(1) - 상수 시간

  • 설명: 입력 크기에 관계없이 항상 일정한 시간이 소요됩니다.
  • 예시: 리스트의 특정 인덱스 접근, 변수의 값 설정 등.

O(log n) - 로그 시간

  • 설명: 입력 크기가 증가할 때, 시간 복잡도가 로그 형태로 증가합니다. 일반적으로 리스트를 반으로 나누는 경우 발생합니다.
  • 예시: 이진 탐색, 특정 조건을 만족하는 값 찾기.

O(n) - 선형 시간

  • 설명: 입력 크기에 비례하여 시간이 증가합니다. 리스트의 모든 요소를 한 번씩 검사해야 할 때 발생합니다.
  • 예시: 리스트의 모든 요소 출력, 단순 검색 등.

O(n²) - 이차 시간

  • 설명: 입력 크기의 제곱에 비례하여 시간이 증가합니다. 중첩 반복문이 있는 경우에 해당합니다.
  • 예시: 버블 정렬, 선택 정렬, 두 리스트의 모든 조합을 비교하는 경우.
반응형