
통계를 공부하다 보면 처음부터 낯선 개념들이 쏟아져 들어온다. Population, Sample, Variable같은 용어부터 Descriptive vs Inferential Statistics까지. 이 글에서는 통계의 기초가 되는 핵심 개념을 간단하게 정리해보려고 한다.
Data (데이터)란 무엇인가?
데이터(Data)란 관찰이나 측정을 통해 얻은 정보다. 숫자일 수도 있고, 분류된 텍스트일 수도 있다. 예를 들어 “키 170cm”, “성별: 여자”, “지역: 토론토” 모두 데이터에 해당한다.
Population, Census, Sample, Variable
Population (모집단)
조사의 출발점이자 중심이 되는 것이 바로 모집단이다. 정의하자면, 어떤 조사가 집중하는 명확하게 정의된 대상 전체를 말한다. 예를 들어, 한 연구에서는 모집단이 특정 기간 동안 생산된 젤라틴 캡슐 전체일 수 있고, 또 다른 조사에서는 가장 최근 학년도에 수학 학사 학위를 받은 모든 사람이 모집단이 될 수 있다. 이번 학기 수학 시험 평균을 구하고 싶다면, 모집단은 해당 과목을 수강한 모든 학생이다. 캐나다 전역 시민들의 평균 소득을 조사하려면? 모집단은 캐나다에 거주하는 모든 시민이 되는 것이다.
즉, 관심 있는 대상 전체가 모집단이며, 조사 목적에 따라 모집단의 범위도 달라진다.
Census (센서스)
센서스는 모집단 전체를 빠짐없이 조사하는 방식이다. 가장 대표적인 예가 바로 국가 인구조사이다. 국가 인구조사는 수년마다 모든 국민을 대상으로 수집되는 데이터다. 하지만 시간과 예산의 제약이 크고, 자료 수집과 처리에 상당한 자원이 소요되기 때문에 대부분의 연구에서 센서스를 수행하기 어렵다.
그래서 보통은 더 현실적인 방법인 ‘샘플링’을 선택하게 된다.
Sample (표본)
샘플은 모집단 전체 중에서 일부를 골라 조사하는 방식이다. 예를 들어 전체 인구 중에서 1,000명을 무작위로 추출해 설문조사를 한다면, 이 1,000명이 바로 샘플이다.
이때 중요한 건 샘플에서 어떤 데이터를 수집할 것인가이다. 우리가 관심을 갖는 것은 모집단 객체의 특정 특성들이고, 이 특성을 변수(variable)라고 부른다.
Variable (변수)

변수(Variable)란, 모집단 내 객체마다 달라질 수 있는 특성이다. 예를 들어, 성별(남/여), 키, 몸무게, 혈압 수치, 졸업 연도 등은 모두 변수에 해당한다.
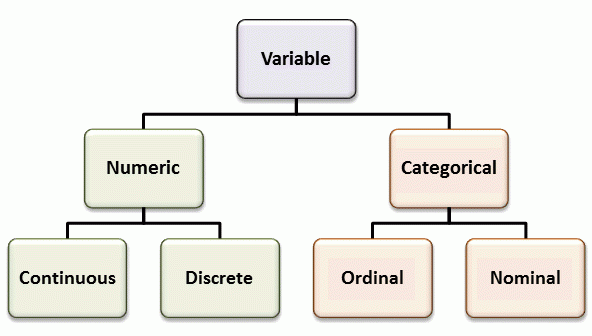
변수는 범주형(categorical) 혹은 수치형(numerical)일 수 있다.
- 범주형 변수: 성별, 전공, 구매한 컴퓨터 종류(Laptop/Desktop) 등
- 수치형 변수: 키, 몸무게, 시험 점수, 혈압 수치 등
예시
예시 1: 제품 품질 조사
- 모집단: 특정 기간에 생산된 모든 젤라틴 캡슐
- 센서스: 해당 기간 생산된 모든 캡슐을 검사 (비현실적)
- 샘플: 무작위로 500개의 캡슐만 검사
- 변수 예시: 캡슐 무게(g), 파손 여부(Yes/No), 유통기한
예시 2: 교육 관련 조사
- 모집단: 2024년 수학 학사 졸업생 전체
- 센서스: 모든 졸업생에게 설문조사
- 샘플: 그 중 200명만 선정해 응답 수집
- 변수 예시: 취업 여부(취업/미취업), 졸업평점(GPA), 졸업 후 진로(업종 카테고리)
통계학의 두 가지 큰 줄기: Descriptive vs. Inferential Statistics
기술통계 (Descriptive Statistics)
데이터를 요약하고 정리하는 데 집중한다. 그래프, 표, 평균, 중앙값, 분산, 표준편차 등 시각적/수치적 요약 도구를 활용해 ‘있는 그대로의 데이터’를 이해하기 쉽게 표현한다.

예를 들어, 한 연구에서 60개 자선 단체의 모금 비용이 총 지출에서 차지하는 비율에 대한 데이터가 있다고 하자. 이 데이터를 아무 정리 없이 숫자 그대로 나열하면 다음과 같은 의문이 생긴다.
- 어떤 값이 가장 일반적일까? (typical value)
- 데이터는 평균값 주변에 몰려 있는가, 흩어져 있는가? (dispersion)
- 특이값이나 결측값, 또는 값들 사이에 빈 구간이 있는가? (gaps, outliers)
이처럼 정리되지 않은 숫자 덩어리만으로는 데이터를 통해 의미 있는 통찰을 얻기 어렵다. 바로 이런 이유 때문에 기술통계는 중요하다.

히스토그램은 데이터의 분포를 직관적으로 보여주는 도구이다. 위의 히스토그램을 통해 데이터를 정리해 보면 다음과 같은 정보가 드러난다.
- 36개 단체(60%)는 모금에 10% 미만의 예산을 사용
- 18개 단체(30%)는 10%에서 20% 사이를 사용
- 즉, 총 54개 단체(90%)가 모금에 20% 미만을 사용
이렇게 히스토그램은 단순히 ‘숫자’를 넘어서, 데이터가 어떤 구간에 얼마나 몰려 있는지, 그리고 어디서부터 ‘이례적’인지 판단할 수 있는 기준선을 제시해 준다.
이 예시는 단순한 숫자 분석을 넘어, 정책적·윤리적 판단으로도 이어진다. 자선단체는 모금을 위해 돈을 써야 하지만, 동시에 그 비용은 실제 수혜자에게 돌아갈 돈을 줄이기도 한다. 그래서 “얼마까지 쓰는 게 적절할까?“는 매우 민감한 문제이다. 히스토그램은 이런 질문에 답을 주진 않지만, “어디까지가 일반적이고, 어디부터가 예외적인가”를 시각적으로 보여준다. 그 다음은 개인의 판단에 달려 있는 것이다.
“나는 모금에 30% 이상 쓰는 단체는 기부하고 싶지 않아.” vs. “운영 효율보다 메시지가 중요한 단체라면 괜찮아.” |
이처럼, 데이터 시각화는 우리 각자가 기준선을 긋는 데 필요한 정보를 제공한다.
추론통계 (Inferential Statistics)
추론 통계(Inferential Statistics)는 표본(sample)을 기반으로 모집단(population) 전체에 대한 결론을 도출하는 데 목적이 있다. 즉, “전체를 다 알 수 없기에, 일부를 통해 전체를 추정하는 기술”이 바로 추론 통계다.
예를 들어, 우리는 한 초등학교 1학년 학생들의 IQ 평균을 알고 싶다. 이때 전체 학생을 조사하지 않고 일부 학생들의 데이터를 통해 분석한 결과, 모집단 평균 (population mean) IQ는 109에서 118 사이일 가능성이 높다는 결론이 나왔다면, 이 숫자 범위가 바로 신뢰 구간이다.
이 신뢰 구간이 전국 평균 IQ인 100보다 확실히 높기 때문에, 해당 학급은 평균 이상이라는 해석이 가능하다.
오늘은 통계의 기본 개념과 기술통계, 추론통계에 대해 간단히 정리했습니다. 다음 글에서는 기술통계에서 많이 쓰이는 시각적 도구와 표 형태에 대해 다뤄보겠습니다!
'Statistics > Probability & Statistics' 카테고리의 다른 글
| 확률과 통계 | 표본공간, 사건, 집합 이론 이해하기 (3) | 2025.07.29 |
|---|---|
| 확률과 통계 | 산포도 이해하기: 표준편차부터 박스플롯까지 (4) | 2025.07.11 |
| 확률과 통계 | 평균(mean), 중앙값(median), 절사평균(trimmed mean) 쉽게 이해하기 (10) | 2025.06.29 |
| 확률과 통계 | 통계 시각화 기초 쉽게 이해하기: 줄기-잎 그림부터 히스토그램까지 (5) | 2025.06.28 |
| 확률과 통계 | 모집단(Population), 표본(Sample), 확률변수(Random Variable) 개념 정리 (1) | 2025.06.26 |