
통계에서 데이터의 분포를 파악하는 것은 매우 중요하다. 이번 글에서는 대표적인 시각적 도구인 줄기-잎 그림(Stem-and-Leaf Plot), 점 그래프(Dotplot), 그리고 히스토그램(Histogram)에 대해 공부해보려 한다.
줄기-잎 그림(Stem-and-Leaf Plot)
줄기-잎 그림은 각 수치를 줄기(stem)와 잎(leaf)으로 나누어 데이터를 정렬된 형태로 표현한다. 실제 값을 그대로 보존하면서 분포를 쉽게 파악할 수 있어, 소규모 정수형 데이터에 자주 사용된다.
줄기-잎 그림 만드는 5단계
- 줄기(Stem)로 사용할 숫자 자릿수를 정한다
- 관측값에서 한 개 또는 여러 개의 앞자리 숫자를 줄기 값으로 선택한다.
- 나머지 뒷자리 숫자가 잎(Leaf)이 된다.
- 가능한 줄기 값들을 세로로 나열한다
- 관측값 범위에 맞는 줄기 값들을 위에서 아래로 적는다.
- 각 관측값의 잎을 해당 줄기 옆에 기록한다
- 관측값마다 잎에 해당하는 숫자를 줄기 옆에 쓴다.
- 줄기 옆 잎들을 오름차순(작은 것 → 큰 것)으로 정렬한다
- 각 줄기마다 잎을 작은 순서로 배열해 분포를 잘 보여준다.
- 줄기와 잎의 단위를 표시한다
- 예를 들어, “줄기 = 10의 자리, 잎 = 1의 자리” 같은 정보를 표시해 해석을 쉽게 한다.
예를 들어, 시험 점수 7개가 있다고 가정하자.
데이터: 93, 84, 86, 78, 95, 81, 72
관측값에서 한 개 또는 여러 개의 앞자리 숫자를 줄기 값으로 선택한다. 여기서는 십의 자리를 줄기 값으로 선택한다. 그 후, 관측값 범위에 맞는 줄기 값들을 위에서 아래로 적는다.
7|
8|
9|
관측값마다 잎에 해당하는 숫자를 줄기 옆에 쓴다.
7|82
8|461
9|35
각 줄기마다 잎을 작은 순서로 배열해 분포를 잘 보여준다.
7|28
8|146
9|35
줄기와 잎의 단위를 표기한다.
7|28
8|146
9|35
줄기: 10의 자리
잎: 1의 자리
예시

이 줄기-잎 그림은 x = 학부생 중 폭음(binge drinking)하는 학생의 비율을 나타낸 140개의 값을 시각화한 것이다. 예를 들어, 줄기 2줄에서 첫 번째 잎이 1이라는 것은 어떤 대학에서는 학부생의 21%가 폭음자였다는 것을 의미한다. 이 표는 전형적이거나 대표적인 값이 줄기 4줄, 즉 40%대 중반임을 시사한다. 관측값들이 이 대표값 근처에 매우 몰려 있지는 않다. 만약 20%~49% 사이에만 값이 있었다면 훨씬 집중됐을 텐데, 실제로는 좀 더 퍼져 있음을 알 수 있다. 아래로 내려가면서 값이 많아지다가 어느 한 지점에서 정점을 찍고, 그 이후로는 다시 줄어든다. 그리고 빈 줄기(빈 구간)이 없다. 즉, 데이터가 비교적 고르게 퍼져 있음을 알 수 있다. 그림의 형태가 완벽하게 대칭은 아니며, 저값(낮은 비율) 쪽으로 약간 더 길게 뻗어 있다. 극단적인 이상치는 없다. 이 데이터에서 가장 놀라운 점은, 대부분의 대학에서 최소 25% 이상이 폭음자라는 사실이다.
줄기-잎 그림을 통해 알 수 있는 것들
- 데이터의 전체 분포 형태
- 데이터가 대칭인지, 한쪽으로 치우쳐 있는지 (→ 정규분포 / 왼쪽 or 오른쪽 꼬리)
- 단봉형(unimodal)인지, 여러 봉우리가 있는지(multimodal)
- 대표값의 위치
- 데이터가 가장 많이 몰려 있는 구간 → 전형적인 값(typical value) 파악 가능
- 줄기 구간 중 잎이 가장 많은 곳이 중심 경향 (예: 평균, 중앙값 근처)
- 산포 정도 (데이터의 퍼짐)
- 줄기 전체 범위를 보면 최솟값 ~ 최댓값, 즉 데이터 범위를 바로 알 수 있음
- 줄기 간격이 넓고 잎이 퍼져 있으면 → 산포가 크다
- 이상치(Outliers)의 존재 여부
- 다른 값들과 동떨어진 잎이 있다면 → 극단값 또는 이상치 의심 가능
- 데이터의 구체적인 값
- 히스토그램과 달리, 개별 숫자 값 자체를 확인 가능
- 예: 7 | 28 → 정확히 72, 78이 있다는 걸 알 수 있음
- 데이터 개수
- 모든 줄기의 잎 개수를 세면 전체 관측값 수(N)를 바로 확인할 수 있음
점 그래프(Dotplot)
점 그래프는 각 데이터 값을 점으로 나타내고, 같은 값은 점을 쌓아 올려 빈도를 보여 준다. 예를 들어, 시험 점수가 70이 세 번 나오면 70 위에 점 세 개를 찍는 방식이다. 점 그래프는 데이터를 간단하게 요약해 빈도와 분포를 한눈에 보여 준다. 다만, 데이터가 많아지면 점이 너무 많아져 복잡해질 수 있다.
예시

대표값은 약 110이며 데이터는 대칭적인 모습을 이루는 편이다.
히스토그램(Histogram)
히스토그램은 데이터를 구간(bins)으로 나누어 각 구간에 속하는 데이터 개수를 막대그래프로 표현한다. 줄기-잎 그림이나 점 그래프보다 더 큰 데이터셋에서 유용하며, 데이터의 분포, 중심, 퍼짐 정도(분산)를 직관적으로 파악할 수 있다. 히스토그램은 연속형 데이터의 분포를 보여주는 데 가장 널리 쓰이는 시각화 도구 중 하나다.
히스토그램은 데이터를 구간별로 나누어 빈도를 시각적으로 표현한다. 하지만 단순한 빈도(frequency)보다 상대빈도(relative frequency)를 사용하는 것이 더 유용할 때도 많다.
상대빈도(Relative Frequency)
상대빈도는 어떤 값이 전체 데이터 중에서 얼마나 자주 나타났는지를 비율로 나타낸 값이다.

즉, 특정 값 x_i의 빈도수/전체 데이터 개수이다.
예를 들어, 200개의 데이터 중에서 값 1이 70번 나타났다면, 값 1의 상대빈도는 70/200 = 0.35이다. 이 말은 즉슨, 전체의 35%가 x = 1이라는 뜻이다.
카운팅 데이터용 히스토그램 그리는 법
히스토그램은 연속형 데이터에만 쓰인다고 생각할 수 있지만, 카운팅 데이터(예: 결함 개수, 고객 수, 전화 건수 등)에도 잘 어울리는 시각화 도구이다.
1. 각 x값의 빈도(Frequency)와 상대빈도(Relative Frequency)를 계산하기
먼저, 데이터에서 각 x값이 몇 번 나왔는지 세고, 그 수를 전체 데이터 개수로 나누어 상대빈도를 구한다.
2. 수평축에 가능한 x값을 표시하기
3. 각 x값 위에 해당하는 상대빈도 높이의 직사각형 그리기
예시
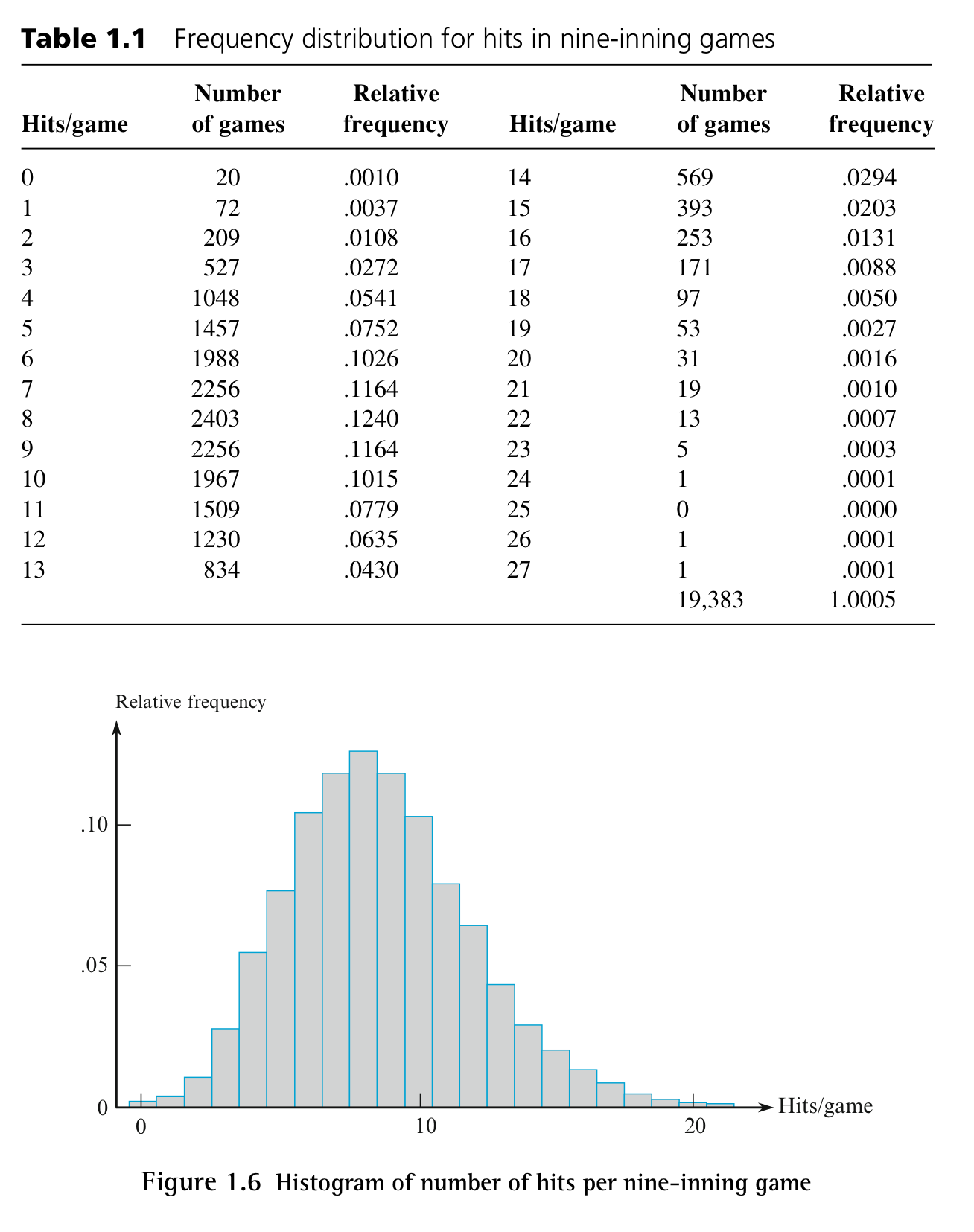
위는 1989년부터 1993년까지의 메이저리그 9이닝 경기 데이터를 바탕으로, 한 팀당 경기당 안타 수(x)에 대한 상대빈도 히스토그램을 해석한 예시이다.
- x = 0 (노히트, no-hitter)인 경기는 전체의 약 0.0015 (0.15%) → 매우 드문 경우
- *x ≥ 22 (22개 이상 안타)도 거의 비슷한 확률로 발생 → 매우 높은 안타 수도 드물다는 의미
- 히스토그램은 오른쪽으로 약간 더 길게 뻗어 있음→ 보통 5~10개 사이가 많지만, 가끔 매우 높은 안타 수가 나오는 경우도 있음 → Positive skew (오른쪽 꼬리가 긴 분포)
측정값을 위한 히스토그램 그리는 법 (동일한 구간 너비(equal class widths))
히스토그램은 연속적인 수치형 데이터(예: 키, 몸무게, 시간 등)를 시각적으로 표현할 때 가장 널리 사용되는 도구이다. 특히 측정값(measurement data)을 사용할 때는 구간을 나누는 방법이 중요하다.
1.각 구간의 빈도 및 상대빈도 계산하기
먼저 데이터를 일정한 너비의 구간(class interval)으로 나누고, 각 구간에 속하는 관측값의 개수(빈도)와 전체 데이터에서의 비율(상대빈도)를 계산한다.
2. 수평축에 구간 경계(class boundaries) 표시하기
측정값이므로 수평축(x축)은 연속적인 측정 단위를 나타낸다.
3. 각 구간 위에 직사각형 그리기
측정값을 위한 히스토그램 그리는 법 (구간 너비가 다른 경우 (Unequal Class Widths))
히스토그램은 일반적으로 일정한 구간 너비를 사용하지만, 특정 상황에서는 구간마다 너비가 달라야 할 때도 있다. 예를 들어, 극단값이 적은 구간을 넓게 설정하거나, 중요한 범위를 좁게 나눠서 더 자세히 보여주고 싶을 때가 그렇다. 이럴 때는 단순히 빈도나 상대빈도로 막대 높이를 정하면 왜곡이 생긴다. 따라서 구간 너비를 고려한 밀도(density) 개념을 사용해야 한다.
1.각 구간의 빈도 및 상대빈도 계산
2.각 구간의 밀도(density) 계산

예시
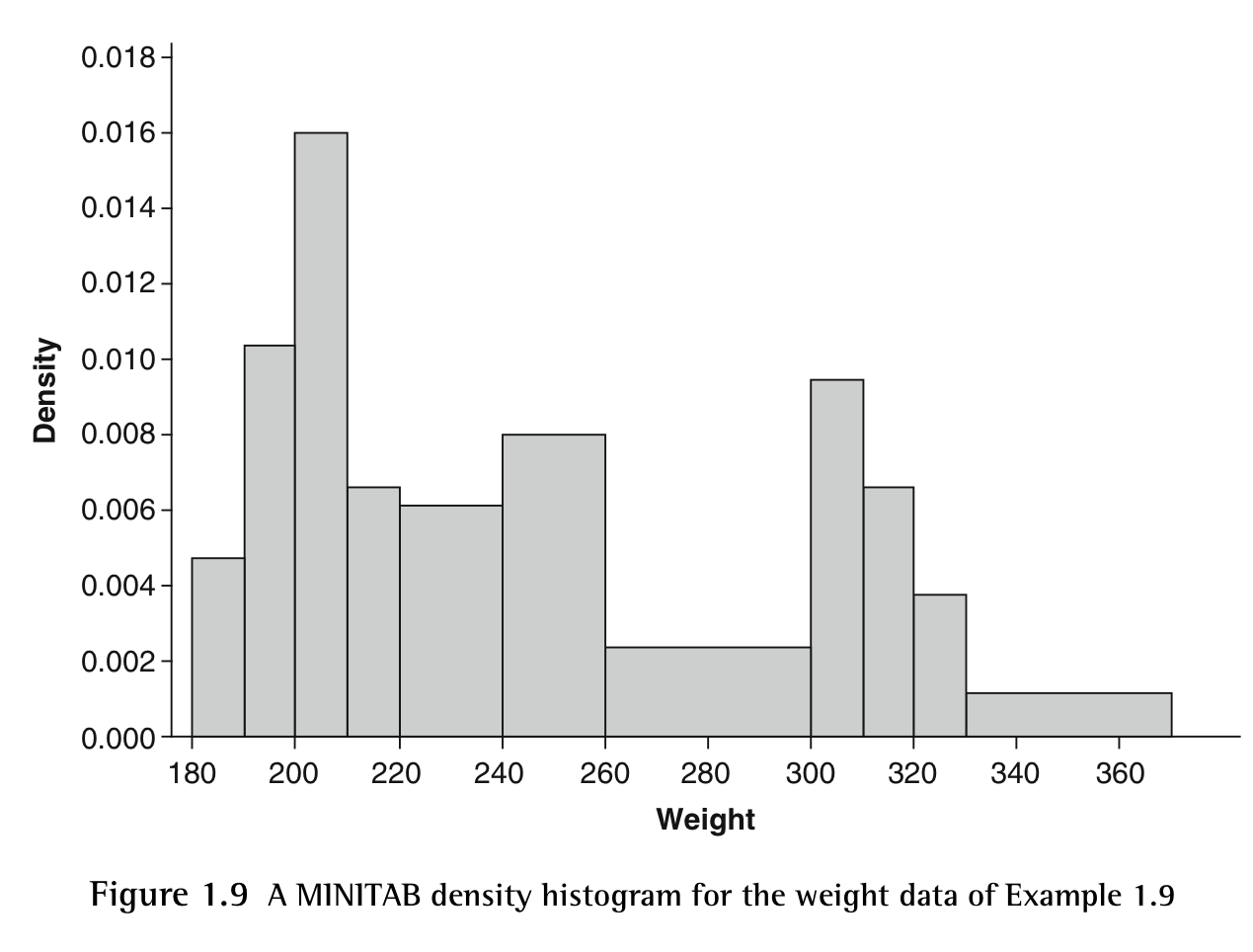
2011년 슈퍼볼에 출전한 두 팀의 모든 선수 106명의 체중 데이터를 이용해 만든 히스토그램을 해석해 봅시다. 이 히스토그램에서는 세 개의 뚜렷한 봉우리(peak)가 관찰된다. 이는 데이터가 단순히 정규분포가 아닌, 다봉형(multimodal) 구조를 갖고 있다는 것을 의미한다.
첫 번째 봉우리: 경량 선수들
- 위치: 체중이 가장 낮은 구간
- 포지션: 디펜시브 백(defensive backs), 와이드 리시버(wide receivers)
- 특징: 민첩성과 속도가 중요한 포지션, 보통 170–200파운드 사이
두 번째 봉우리: 중간 체중 선수들
- 위치: 중간 구간
- 포지션: 라인배커(linebackers), 러닝백(running backs)
- 특징: 스피드와 힘의 균형이 중요한 포지션, 약 210–240파운드
세 번째 봉우리: 중량급 선수들
- 위치: 체중이 가장 높은 구간
- 포지션: 오펜시브 라인, 디펜시브 라인
- 특징: 충돌과 힘이 요구되는 포지션, 보통 300파운드 이상
히스토그램의 모양
히스토그램은 단순히 데이터의 크기만 보여주는 게 아니라, 데이터의 분포 형태(Shape of Distribution)도 시각적으로 전달한다. 그 분포의 모양을 통해 우리는 데이터의 중심, 퍼짐, 왜도(비대칭성) 등을 알 수 있다.
봉우리(Peak)의 개수
Unimodal
- 하나의 뚜렷한 중심(peak)이 있는 분포
- 예: 시험 점수가 평균 근처에 몰린 경우
Bimodal
- 두 개의 봉우리가 있는 분포
- 예: 두 다른 집단이 섞인 경우 (예: 남/여 키)
Multimodal
- 세 개 이상의 봉우리가 있는 분포
- 예: 포지션별 체형이 다른 운동선수 집단 (앞서 본 NFL 체중 히스토그램이 그 예!)
대칭성 (Symmetry)
대칭 (Symmetric)
- 왼쪽과 오른쪽이 거의 비슷한 모양
- 예: 정규분포 (bell-shaped)

오른쪽으로 긴 분포 (Positively Skewed / Right Skewed)
- 꼬리(Tail)가 오른쪽으로 길게 늘어짐
- 예: 소득 분포 (대부분은 적지만 일부 고소득자가 있음)
왼쪽으로 긴 분포 (Negatively Skewed / Left Skewed)
- 꼬리가 왼쪽으로 길게 늘어짐
- 예: 대부분 학생이 높은 점수를 받았을 때 시험 점수 분포

다음 글에서는 데이터의 위치를 대표하는 여러 통계량에 대해 다룰 예정입니다. 평균, 중앙값, 최빈값 등 데이터를 대표하는 값들이 무엇인지, 그리고 각각의 특징과 활용 방법을 살펴보겠습니다.
'Statistics > Probability & Statistics' 카테고리의 다른 글
| 확률과 통계 | 표본공간, 사건, 집합 이론 이해하기 (3) | 2025.07.29 |
|---|---|
| 확률과 통계 | 산포도 이해하기: 표준편차부터 박스플롯까지 (4) | 2025.07.11 |
| 확률과 통계 | 평균(mean), 중앙값(median), 절사평균(trimmed mean) 쉽게 이해하기 (10) | 2025.06.29 |
| 확률과 통계 | 꼭 알아야 할 핵심 개념: 모집단부터 추론통계까지 (3) | 2025.06.27 |
| 확률과 통계 | 모집단(Population), 표본(Sample), 확률변수(Random Variable) 개념 정리 (1) | 2025.06.26 |