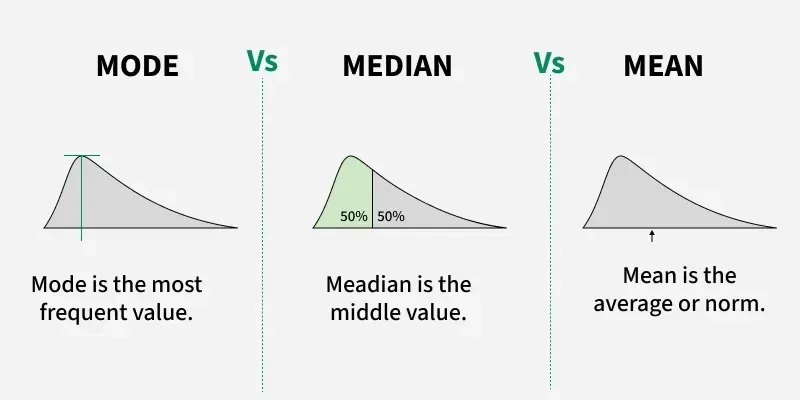
평균(mean)과 중앙값(median)은 데이터가 어디쯤 중심을 이루는지 보여주는 수치이다. 이번 글에서는 이 두 가지 중심 위치 척도뿐만 아니라, 극단값(outlier)에 대한 민감도, 그리고 이를 보완해주는 절사 평균(trimmed mean)까지 함께 살펴본다.
평균값(mean)과 중앙값(median)
- 평균 (Mean): 모든 값을 더해 개수로 나눈 값.
- 중앙값 (Median): 데이터를 정렬했을 때 정확히 가운데에 위치한 값.
둘 다 데이터의 중심을 나타내지만, 데이터 분포가 비대칭이거나 극단값(outlier)이 존재할 경우 서로 다른 이야기를 한다.
그리고 실제 통계 분석에서는 전체 모집단의 데이터를 알 수 없는 경우가 많기 때문에 표본(sample)을 사용한다. 이때 나오는 개념은 표본 평균(sample mean)과 표본 중앙값(sample median)이다.
- 표본 평균 (Sample Mean, x̄): 표본의 모든 값을 더한 후 표본 개수로 나눈 값

- 표본 중앙값 (Sample Median): 표본을 정렬했을 때 가운데 위치한 값 (~ 표시를 사용함)

이 값들은 각각 모집단 평균(Population Mean, μ, 뮤)과 모집단 중앙값(Population Median)의 추정값 역할을 하며, 실제 데이터 분석에서 모집단의 중심 위치를 추정하는 데 핵심적인 역할을 한다.
극단값(outlier)에 대한 민감도
평균은 모든 값을 반영하는 계산 방식이기 때문에 극단값의 영향을 크게 받는다.

위의 데이터를 보면 95는 명백한 극단값임을 알 수 있다. 이 값을 포함한 평균값은 67이다. 이 극단값을 제외하고 평균값을 계산하면 65.7이 된다, 이로 인해 극단값 하나가 평균을 1.3만큼 끌어올렸다는 사실을 알 수 있다. 이처럼 평균은 전체적인 경향을 보여주는 데 유용하지만, 데이터에 outlier가 있을 경우 중심 위치를 왜곡할 위험이 크다.
반면, 중앙값은 데이터의 크기 순서에서 ‘위치’만 고려하기 때문에, 크기가 극단적으로 큰 값이 포함되더라도 중앙값 자체는 흔들리지 않는다. 즉, 중앙값은 데이터가 비대칭이거나 이상값이 포함되어 있을 때에도 안정적인 중심값으로 사용될 수 있다. 그래서 극단값의 영향을 최소화하고 싶을 때는 중앙값이 평균보다 더 신뢰할 수 있는 선택이 된다.
모집단 분포의 세 가지 형태와 평균·중앙값의 관계
데이터가 어떤 분포를 따르는지에 따라 평균과 중앙값의 상대적 위치가 달라진다.

a. 왼쪽으로 치우친 분포 (Left-skewed Distribution)
- 예: 시험에서 대부분이 높은 점수를 받았을 때
- 모집단 평균 < 모집단 중앙값
- 극단적으로 작은 값이 존재하여 평균이 왼쪽으로 끌려간다.
- 예를 들어 대부분 학생이 90점 이상인데 한두 명만 20점이라면, 평균은 낮아지지만 중앙값은 여전히 높게 유지된다.
데이터: [20, 25, 90, 91, 92, 93, 94]
- 평균 = (20 + 25 + 90 + 91 + 92 + 93 + 94) / 7 = 72.14
- 중앙값 = 91
평균은 더 많이 내려가지만, 중앙값은 소수의 outlier에 여전히 강한 모습을 보임.
b. 대칭 분포 (Symmetric Distribution)
- 예: 정규분포(normal distribution)
- 모집단 평균 ≈ 모집단 중앙값
- 데이터가 중심을 기준으로 좌우 대칭일 때, 평균과 중앙값은 거의 같은 위치에 있다.
- 정규분포에서는 평균, 중앙값, 최빈값이 모두 동일한 지점에 위치함.
데이터: [90, 91, 92, 93, 94, 95, 96]
- 평균 = (90 + 91 + 92 + 93 + 94 + 95 + 96) / 7 = 93
- 중앙값 = 93
평균과 중앙값이 같다.
c. 오른쪽으로 치우친 분포 (Right-skewed Distribution)
- 예: 소득 분포, 부동산 가격
- 모집단 평균 > 모집단 중앙값
- 극단적으로 큰 값이 일부 존재하여 평균이 오른쪽으로 끌려간다.
- 평균이 “outlier”에 의해 더 큰 방향으로 밀리는 것을 볼 수 있다.
데이터: [40, 45, 50, 52, 53, 55, 200]
- 평균 = (40 + 45 + 50 + 52 + 53 + 55 + 200) / 7 = 70.7
- 중앙값 = 52
평균은 증가, 하지만 중앙값은 변함 없음.
Trimmed Mean: 평균과 중앙값 사이의 절충안
절사 평균(Trimmed Mean)은 상위/하위 극단값 일부를 제거한 후 평균을 계산한다.
예: 10% trimmed mean은 양쪽 10%씩 잘라낸 뒤 평균을 계산
- 평균보다 극단값에 덜 민감하고
- 중앙값보다 더 많은 정보를 활용함
즉, 평균과 중앙값 사이에서 균형 잡힌 위치 척도 역할을 한다.
만약 범주형 데이터라면?
범주형 데이터는 서로 구분되는 범주(category)로 나뉘는 데이터를 뜻한다. 예를 들어, 성별(남자/여자), 혈액형(A/B/O/AB), 좋아하는 색깔(빨강/파랑/초록) 등이 모두 범주형 데이터다. 범주형 데이터는 숫자로 된 데이터와 달리 ‘크다/작다’를 비교하는 것이 아니라, 각 범주에 속하는 데이터의 빈도 또는 비율을 분석하는 데 초점을 둔다.
모비율(p)과 표본 비율(𝑝̂)의 관계
범주형 데이터 분석에서는 표본 비율 𝑝̂ = x/n 이 매우 중요한 역할을 한다. 이 값은 전체 표본 중 특정 범주에 속하는 비율을 나타낸다.
그렇다면 모비율 p는 무엇일까?
이는 전체 모집단(population)에서 특정 범주에 속하는 비율을 의미하며, 𝑝̂와 마찬가지로 항상 0과 1 사이의 값을 가진다.
이 둘의 관계는 마치 다음과 같다
- 𝑝̂ ↔ p
- x̄ (표본 평균) ↔ μ (모평균)
즉, 𝑝̂는 우리가 모집단 비율 p를 추정(estimation)하기 위해 사용하는 점 추정치(point estimate)다.
예를 들어, 어떤 조사에서 자동차 소유자 100명을 대상으로 “차를 5년 이상 보유한 적이 있나요?”라고 물었을 때, 22명이 “그렇다”고 응답했다면, 그에 대한 표본 비율은 𝑝̂ = 22/100 = 0.22 이다.
이 0.22는 모든 자동차 소유자 중 5년 이상 같은 차를 보유한 사람의 비율 p에 대한 점 추정치(point estimate)가 된다.
즉, 이 데이터를 통해 우리는 전체 자동차 소유자 중 약 22% 정도가 5년 이상 차를 보유했을 것이라고 추정할 수 있는 것이다.
이러한 개념은 나중에 신뢰구간(confidence interval)이나 가설 검정(hypothesis test)을 수행할 때 핵심적인 기반이 된다.
이번 글에서는 데이터의 중심을 이해하는 다양한 방법들을 살펴보았습니다. 하지만 중심만으로는 데이터의 전체적인 성격을 완전히 파악할 수는 없습니다. 다음 글에서는 데이터가 얼마나 흩어져 있는지, 퍼져 있는지를 알려주는 variability(산포도)에 대해 알아보겠습니다!
이전 글 보러가기
2025.06.28 - [Statistics/Probability & Statistics] - 확률과 통계 | 통계 시각화 기초 쉽게 이해하기: 줄기-잎 그림부터 히스토그램까지
확률과 통계 | 통계 시각화 기초 쉽게 이해하기: 줄기-잎 그림부터 히스토그램까지
통계에서 데이터의 분포를 파악하는 것은 매우 중요하다. 이번 글에서는 대표적인 시각적 도구인 줄기-잎 그림(Stem-and-Leaf Plot), 점 그래프(Dotplot), 그리고 히스토그램(Histogram)에 대해 공부해보려
olivecodelab.tistory.com
2025.06.27 - [Statistics/Probability & Statistics] - 확률과 통계 | 꼭 알아야 할 핵심 개념: 모집단부터 추론통계까지
확률과 통계 | 꼭 알아야 할 핵심 개념: 모집단부터 추론통계까지
통계를 공부하다 보면 처음부터 낯선 개념들이 쏟아져 들어온다. Population, Sample, Variable같은 용어부터 Descriptive vs Inferential Statistics까지. 이 글에서는 통계의 기초가 되는 핵심 개념을 간단하게
olivecodelab.tistory.com
'Statistics > Probability & Statistics' 카테고리의 다른 글
| 확률과 통계 | 표본공간, 사건, 집합 이론 이해하기 (3) | 2025.07.29 |
|---|---|
| 확률과 통계 | 산포도 이해하기: 표준편차부터 박스플롯까지 (4) | 2025.07.11 |
| 확률과 통계 | 통계 시각화 기초 쉽게 이해하기: 줄기-잎 그림부터 히스토그램까지 (5) | 2025.06.28 |
| 확률과 통계 | 꼭 알아야 할 핵심 개념: 모집단부터 추론통계까지 (3) | 2025.06.27 |
| 확률과 통계 | 모집단(Population), 표본(Sample), 확률변수(Random Variable) 개념 정리 (1) | 2025.06.26 |