
통계에서 데이터의 중심(평균, 중앙값 등)을 파악하는 것만으로는 부족하다. 데이터가 얼마나 퍼져 있는지, 즉 산포(variability)를 함께 이해해야 데이터 전체의 특성을 제대로 해석할 수 있다.
이번 글에서는 산포를 측정하는 대표적인 지표들과 함께, boxplot과 이상치(outlier) 해석까지 다루어 보겠다.
왜 평균만으로는 부족할까?
데이터 분석에서 평균(mean)이나 중앙값(median) 같은 중심 경향치(measures of center)는 중요한 정보를 제공한다. 하지만 이들만 보고 전체 데이터의 특성을 완전히 이해하기는 어렵다.
“평균이 같다고 해서 데이터가 같다고 말할 수는 없다!”
예를 들어,
- 샘플 A: 5, 5, 5
- 샘플 B: 1, 5, 9
- 샘플 C: 0, 5, 10
이 세 샘플은 모두 평균이 5이고 중앙값도 5이다. 하지만 숫자들의 퍼짐 정도, 즉, 산포는 다르다.
- 샘플 A는 모든 값이 동일해서 산포가 0
- 샘플 B는 중간 정도로 퍼져 있고
- 샘플 C는 가장 넓게 퍼져 있음
따라서 “중심 + 산포”를 함께 살펴봐야 데이터의 특성과 신뢰도를 제대로 이해할 수 있다.
데이터가 평균을 기준으로 얼마나 흩어져 있는가? 그걸 알려주는 것이 바로 산포(variability)이다.
Range (범위)
가장 간단한 산포 지표이다.
Range = 최대값 − 최소값
Range(범위)는 계산이 간단해서 통계 초입에서 자주 등장하지만, 단점도 분명하다. 바로, 오직 두 개의 값, 최댓값과 최솟값만 사용한다는 점이다.
“나머지 n − 2개의 값이 어디에 있든, range는 변하지 않는다.”
예를 들어 보자
- 샘플 1: 10, 30, 50, 70, 90
- 샘플 2: 10, 11, 12, 13, 90
이 두 샘플의 range는 90 - 10 = 80으로 동일하다. 하지만 데이터의 퍼짐(산포)은 매우 다르다.
- 샘플 1은 값들이 넓게 퍼져 있음
- 샘플 2는 90을 제외하면 모두 10~13 사이에 밀집되어 있음
즉, 샘플 2는 극단값 하나(90) 때문에 range가 커졌지만, 실제 데이터의 대부분은 거의 모여 있는 상태인 것이다. 이런 이유로, range는 이상치(outlier)에 매우 민감하고, 데이터의 전반적인 분포를 제대로 반영하지 못하는 경우가 많다.
Deviations from the Mean (평균으로부터의 편차)
데이터가 평균을 중심으로 얼마나 퍼져 있는지를 알아보려면, 각 관측값이 평균에서 얼마나 멀리 떨어져 있는지를 살펴봐야 한다. 이를 위해 계산하는 것이 바로 편차(deviation)이다.
편차 = xᵢ − x̄
(x̄는 평균, xᵢ는 각 관측값)
- xᵢ > x̄ → 편차는 양수 (평균보다 큼)
- xᵢ < x̄ → 편차는 음수 (평균보다 작음)
모든 편차가 작으면 관측값들이 평균 근처에 몰려 있다는 뜻이고, 편차가 크면 평균에서 멀리 떨어진 값들이 많다는 의미이다.
예시 1. 편차가 작은 경우
데이터: 48, 49, 50, 51, 52
평균 x̄ = 50
각 관측값에서 평균을 뺀 편차는
- 48 − 50 = −2
- 49 − 50 = −1
- 50 − 50 = 0
- 51 − 50 = +1
- 52 − 50 = +2
→ 모든 값이 평균인 50을 중심으로 ±2 이내에 있음 → 변동이 적다
예시 2. 편차가 큰 경우
데이터: 20, 35, 50, 65, 80
평균 x̄ = 50
편차는
- 20 − 50 = −30
- 35 − 50 = −15
- 50 − 50 = 0
- 65 − 50 = +15
- 80 − 50 = +30
→ 값들이 평균에서 멀리 떨어져 있음 → 변동이 크다
하지만 이 편차들을 단순히 더하면 항상 0이 되어버린다.


이를 해결하기 위해, 모든 편차를 제곱해서 음수가 되지 않도록 만들어 줘야 한다.

표본 분산(sample variance)과 표본 표준편차(sample standard deviation)

표본 분산은 각 데이터가 표본 평균(x̄)에서 얼마나 떨어져 있는지를 제곱하여 평균 낸 값이다. 데이터가 평균 근처에 몰려 있으면 분산이 작고, 멀리 흩어져 있으면 분산이 크다.
표본 분산의 단위는 원래 데이터 단위의 제곱이다. 이를 다시 원래 단위로 되돌리기 위해, 표본 분산에 제곱근을 취한 것이 바로 표본 표준편차다.
표본 표준편차 s는 단순히 수식을 계산해 나오는 값이 아니라, 데이터가 평균에서 얼마나 떨어져 있는지를 직관적으로 알려주는 지표다. 예를 들어 다음과 같은 경우를 생각해 보자.
예시: 자동차 연비 데이터
- 표본 1: 어떤 자동차 모델들의 연비(mpg, miles per gallon)를 조사한 결과, 표준편차 s = 2.0 mpg가 나왔다고 하자.
- 이는 각 자동차의 연비가 평균 연비에서 보통 ±2.0 mpg 정도 떨어져 있다는 뜻이다.
- 표본 2: 또 다른 자동차 모델들의 연비를 조사했더니 s = 3.0 mpg였다.
- 이 경우는 평균으로부터 ±3.0 mpg 정도로 더 퍼져 있다는 뜻이며, 이는 표본 1보다 약 1.5배 더 큰 변동성(산포)을 가진다는 해석이 가능하다.
즉, 표준편차는 “전형적인 편차(typical deviation)”를 나타낸다. 어떤 데이터 xᵢ는 평균보다 더 가까이 있을 수도 있고 더 멀리 있을 수도 있지만, s는 그 전형적인 거리의 크기를 보여준다.
모집단 분산(Population Variance)
모집단 분산은 모집단 전체의 데이터가 평균으로부터 얼마나 퍼져 있는지를 나타내는 지표다. 표본 분산이 아닌 모집단 전체에 대한 수치를 다룬다는 점에서 차이가 있다.

왜 표본 분산은 n-1로 나눌까?
우리가 실제로 모집단의 평균(μ)을 알고 있다면, 표본 분산을 계산할 때 각 관측값 xᵢ와 μ의 차이를 제곱해서 평균을 내면 된다. 이때는 분모로 n을 사용해도 전혀 문제가 없다.
하지만 현실에서는 모집단 평균 μ를 모르는 경우가 대부분이다. 그래서 표본 평균(𝑥̄)을 대신 사용해서 각 xᵢ의 편차를 계산하게 된다. 문제는, 이렇게 하면 관측값들이 평균 𝑥̄ 주변에 더 가까이 몰리는 경향이 생겨 분산이 과소추정되는 문제가 생긴다는 것이다.
이 과소추정을 보정하기 위해 분모를 n이 아니라 n−1로 설정한다. 즉, “덜 나누면 값이 커지니까” 작게 나오는 분산을 살짝 키워주는 역할을 하는 것이다. 이것을 자유도(degrees of freedom)라고 부른다.
자유도(Degrees of Freedom, df)
“자유도”라는 개념은 통계학을 처음 배우는 사람들에게 꽤 낯설게 느껴질 수 있다. 밑의 예시를 살펴보자.
예시
친구 A, B, C, D 네 명이 함께 식당에 갔고, 총 식사비는 100달러였다.
이때,
- A가 20달러 냈다고 했고,
- B가 30달러 냈다고 했고,
- C가 10달러 냈다고 함.
그럼 D는 얼마 냈을까?
답은 자동으로 40달러다. 왜냐하면 총액(100달러)이 이미 정해져 있기 때문에 A, B, C의 값을 알고 나면 D는 반드시 그 차액을 내야 하는 것이다.
즉, A, B, C는 자유롭게 정할 수 있었지만, D는 자동으로 결정된다.
자유도(degrees of freedom)는 전체 데이터 중에서, 제약 조건 없이 자유롭게 바꿀 수 있는 값의 개수다.
위 예시에선 총 4명 중 3명만 자유롭게 금액을 정할 수 있었고, 마지막 1명은 총합이 정해져 있어서 자동 결정됐다. 그래서 자유도는 4 − 1 = 3이다.
우리가 분산(또는 표준편차)을 계산할 때, 모집단의 평균(μ)을 모르니까, 표본 평균(x̄)을 대신 사용한다. 근데 이 x̄이 고정돼 있다는 건, 전체 데이터 중 하나는 이미 정해진 평균을 만족하도록 자동 결정된다는 뜻이다. 그래서 표본의 분산은 자유도 n − 1로 나누어야 모집단의 분산을 과소추정하지 않고, 정확하게 추정할 수 있게 된다.
표본 분산을 더 쉽게 계산하는 방법

위의 공식은 매번 x̄을 계산하고, 모든 (xᵢ - x̄)²을 다시 계산해야 하기 때문에 번거롭다. 그래서 계산을 조금 더 효율적으로 하기 위해
Computing Formula (계산 공식) 이 사용된다.

Boxplot (박스플롯)
Boxplot(박스플롯)은 데이터의 분포와 이상치(outlier)를 한눈에 보여주는 시각화 도구다. 사분위수(quartiles) 개념을 기반으로 하며, 데이터의 중심, 퍼짐, 왜도, 극단값 등을 직관적으로 파악할 수 있어 매우 유용하다.
- 데이터 정렬: 관측값을 작은 순서대로 정렬
- 중앙값(Median): 정렬된 데이터의 중심값 - 관측값 개수가 홀수면 가운데 값 하나, 짝수면 가운데 두 수의 평균
- Lower Fourth (Q1): 하위 25% 지점의 중앙값
- 중앙값보다 작은 절반의 데이터에서 다시 중앙값을 구함
- Upper Fourth (Q3): 상위 25% 지점의 중앙값
- 중앙값보다 큰 절반의 데이터에서 중앙값을 구함
📌 중앙값은 데이터 개수가 홀수일 경우, 상·하위 절반에 모두 포함
Fourth Spread = Upper Fourth − Lower Fourth = Q3 − Q1
이 값은 전체 데이터 중 중간 50%의 범위를 의미하며, 흔히 IQR (Interquartile Range)이라고도 불린다.
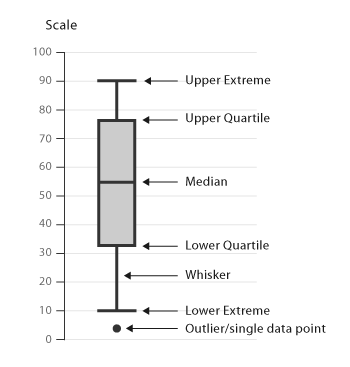

- Median이 박스 중앙: 대칭적 분포 (Symmetric)
- Median이 왼쪽에 치우침: 오른쪽 꼬리 → Positive skew
- Median이 오른쪽에 치우침: 왼쪽 꼬리 → Negative skew
Outliers(이상치)
박스플롯의 중요한 기능 중 하나는 이상치(outliers)를 시각적으로 드러내는 것이다. 이상치는 대부분의 데이터와 동떨어진 극단적인 값으로, 데이터 분석 시 주의 깊게 해석해야 한다.
박스플롯에서는 사분위수(Q1, Q3)를 기반으로 수학적인 기준을 사용해 이상치를 판별한다. 이때 핵심은 IQR (Interquartile Range), 즉 Fourth Spread라고도 부르는 Q3 - Q1다.


위는 암에 걸린 사람들(Cancer group)과 암에 걸리지 않은 사람들(No cancer group)을 대상으로 라돈 노출량을 측정한 데이터를 박스플롯으로 시각화한 예시다.
1. 박스 길이(=IQR)의 차이
- No cancer 그룹의 박스가 더 넓게 퍼져 있음 → 즉, 데이터가 더 다양하게 퍼져 있고 산포(variability)가 크다는 뜻.
- 반대로 Cancer 그룹의 박스는 짧고 조밀함 → 라돈 노출값들이 비교적 일정한 범위 내에 집중되어 있다는 의미.
2. 중앙값(Median)의 위치 차이
- No cancer 박스 안에서 중앙값 선이 왼쪽으로 치우쳐 있음 → 왼쪽으로 왜도(Negative skewness)가 있다는 것을 암시.
- Cancer 박스는 중앙값이 박스 중앙에 가깝고 대칭적 → 중간 50%의 데이터가 고르게 분포되어 있다는 뜻.
3. 겹치는 구간과 라돈 노출량
- Cancer 박스 전체가 No cancer 박스 안에 포함됨 → “암에 걸린 사람이 더 많은 라돈에 노출되었을 것”이라는 가설이 박스플롯만 보면 뚜렷하지 않음
- 이상치(outliers)를 제외하면 최댓값과 최솟값도 거의 차이 없음
이번 글에서는 range, 편차, 분산, 표준편차, 박스플롯, 이상치 등 다양한 개념을 예제와 함께 다뤄봤습니다. 통계 분석을 더 깊이 있게 하기 위해서는 “중심 + 산포”를 함께 읽는 눈이 필요합니다.
다음 글에서는 확률의 기초 개념인 Sample Spaces and Events (표본공간과 사건)을 공부해 보겠습니다!
이전 글 보러가기
확률과 통계 | 평균(mean), 중앙값(median), 절사평균(trimmed mean) 쉽게 이해하기
평균(mean)과 중앙값(median)은 데이터가 어디쯤 중심을 이루는지 보여주는 수치이다. 이번 글에서는 이 두 가지 중심 위치 척도뿐만 아니라, 극단값(outlier)에 대한 민감도, 그리고 이를 보완해주는
olivecodelab.tistory.com
확률과 통계 | 통계 시각화 기초 쉽게 이해하기: 줄기-잎 그림부터 히스토그램까지
통계에서 데이터의 분포를 파악하는 것은 매우 중요하다. 이번 글에서는 대표적인 시각적 도구인 줄기-잎 그림(Stem-and-Leaf Plot), 점 그래프(Dotplot), 그리고 히스토그램(Histogram)에 대해 공부해보려
olivecodelab.tistory.com
확률과 통계 | 꼭 알아야 할 핵심 개념: 모집단부터 추론통계까지
통계를 공부하다 보면 처음부터 낯선 개념들이 쏟아져 들어온다. Population, Sample, Variable같은 용어부터 Descriptive vs Inferential Statistics까지. 이 글에서는 통계의 기초가 되는 핵심 개념을 간단하게
olivecodelab.tistory.com
'Statistics > Probability & Statistics' 카테고리의 다른 글
| 확률과 통계 | 표본공간, 사건, 집합 이론 이해하기 (3) | 2025.07.29 |
|---|---|
| 확률과 통계 | 평균(mean), 중앙값(median), 절사평균(trimmed mean) 쉽게 이해하기 (10) | 2025.06.29 |
| 확률과 통계 | 통계 시각화 기초 쉽게 이해하기: 줄기-잎 그림부터 히스토그램까지 (5) | 2025.06.28 |
| 확률과 통계 | 꼭 알아야 할 핵심 개념: 모집단부터 추론통계까지 (3) | 2025.06.27 |
| 확률과 통계 | 모집단(Population), 표본(Sample), 확률변수(Random Variable) 개념 정리 (1) | 2025.06.26 |